Normal distribution (also known as standard distribution) simply refers to one of the most prevalent data patterns, where the most commonly-occurring value is in the middle of the graph and then the frequency tapers off at either extreme end. For example, if you are looking at home prices in an area, there will be a lot of homes around the average price, which is somewhere in the middle of the graph. Then, as you look for homes that are cheaper and cheaper, or more pricier and pricier, there will be less and less homes available as you go lower or higher in price. In other words, your graph might look something like this:
Get Your CPCU 500 Study Materials NOW!
As you can imagine, this type of pattern (where the most commonly-occurring value is in the middle and then they taper off as you get to either extreme) is true of lots of data sets: human height, 1-mile run times, the list goes on and on. Because of how often you see this pattern, that is why it is worth studying.
Now, the key to understanding how it works is to remember that the following points about a normal distribution graph are always true:
- The mean (average) value of the group is always right in the middle, at 50%.
- The percentages & number of standard deviations separating each “chunk” are always exactly as shown below. (Note: For an explanation of standard deviations, see our other post HERE)
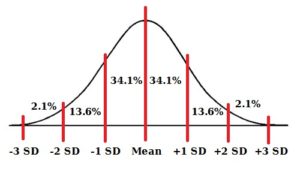
This fact that the graph always follows this pattern and percentages means that if you’re dealing with a normal distribution and you have only a few details, it is really easy to figure out the missing pieces!
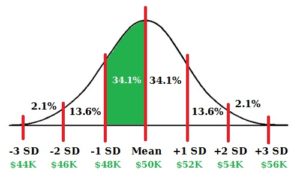
Since the standard deviations is $2,500, that means $35,000 is -2 deviations away from $40,000. You can then add the “chunks” that represent each deviation (34.1% + 13.6% = 47.7%) to get the total percentage that falls within that range.
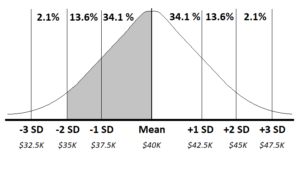
- Draw out the base model
- Shade in the “chunk(s)” the problem is asking you about
- Plug in what you know
- Easily calculate everything else!
Get Your CPCU 500 Study Materials NOW!
1) FOCUS ON THE RIGHT THINGS
We condense every chapter to a few pages each, so you can focus on what you need to know.
2) UNDERSTAND THE KEY CONCEPTS
We provide extra examples & bonus materials to help you understand the trickier concepts.
3) SEE HOW IT ALL RELATES
Our outlines are super organized and make it easy to see how the concepts relate to each other.
Get Your CPCU 500 Study Materials NOW!
Disclaimers: The Institutes, CPCU®, and AINS® are trademarks of the American Institute For Chartered Property Casualty Underwriters, d/b/a The Institutes. InsuranceExamGuides.com is not affiliated or associated with The Institutes in any way, and The Institutes do not endorse, approve, support, or otherwise recognize InsuranceExamGuides.com or its products or services. CPCU® and AINS® are registered trademarks of The Institutes. All rights reserved.